-복소수(Complex Number)란?
복소수는 실수와 허수를 포괄하는 수이다. 복소수는 실수부와 허수부를 나누어 표현할 수 있다.

허수는 실수가 아닌 복소수를 의미하는데, 이 허수의 등장은 복소수평면을 만든 결정적인 계기이다.
이 때, 복소평면이란 x축이 실수축 y축이 허수축인 좌표평면을 말한다.
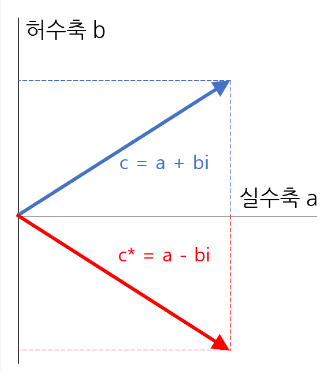
물리학에서 힘은 크기와 방향을 가지는데, 이를 벡터가 아닌 복소수 형식으로 표현하는 것이 가능하다.
복소수는 주로 2차원의 수를 나타내는 데에 쓰이지만 벡터는 다차원으로 확대가 가능하다는 점에서 차이가 있다. 복소수가 2차원만 가능한 것이냐 하면 그건 아니다. 그러나 다차원적을 표현하는 관점에서는 벡터가 유리하다는 것이다.
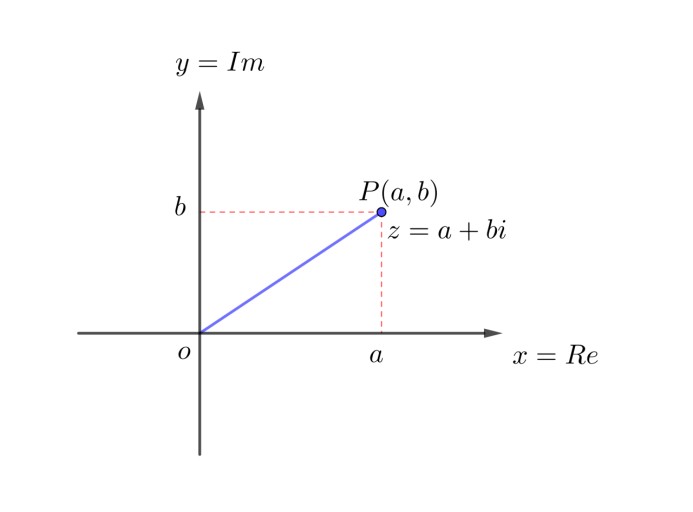
a+bi를 복소평면에 나타내면 마치 원점을 시점으로 하고 점 P를 종점으로 하는 하나의 벡터와 모습이 유사하고, 방향도 존재하는 것처럼 보인다. 즉 직관적으로 봤을 때 복소수 OP는 벡터의 모양을 하고 있다.
-사원수란?
사원수란 4차원 복소수를 의미하는데, 스칼라와 벡터의 합이라 할 수 있다.
영국의 수학자 해밀턴은 복소수를 연구하여 복소수 너머의 수인 사원수를 정립했다.복소수가 복소평면 속 하나의 점으로 나타낼 수 있다는 사실로부터 출발하여 3차원 공간에서 점을 표현하는 방법을 찾는 과정에서 만들어졌다.
a, b, c, d 네 개의 실수 성분을 가지며, 덧셈과 곱셈의 결합법칙, 덧셈의 교환법칙은 성립하지만 곱셈의 교환법칙은 성립하지 않는다.( i x j 와 j x i는 다른 값이다)
복소수와 달리 사원수끼리는 곱셈의 교환법칙이 성립하지않는다.
사원수의 사용
사원수는 공간에서 회전을 표현할 때 사용한다.
기존에 사용하던 행렬, 오일러 각 체계를 사용할 때 발생할 수 있는 짐벌락 현상(gimbal lock)을 없애기 위해 사용하기 시작했다.
짐벌락 현상이란 돌아가는 3개의 짐벌(고리)로 회전을 표현할 때 두 짐벌이 겹쳐지는 순간 하나의 짐벌에 대한 자유도를 상실하게 되는 현상이다.
오일러 각 체계는 3차원 공간의 회전을 할 때 각각을 좌표계의 회전으로 이해하는 방식이다.
이 경우 직관적인 축의 회전으로 이해하긴 쉽지만, 세 축이 서로에 대해 종속적이라(한 축을 돌리면 다른 축도 같이 돈다) 한 축을 돌리던 중 다른 두 축이 겹쳐지는 경우가 발생한다.
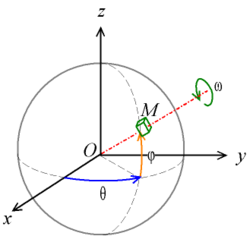
사원수는 이러한 문제를 해결하기 위한 방법으로 사용된다.
https://en.wikipedia.org/wiki/Gimbal_lock
https://naver.me/G5QfJ5ZY
'C# 기초 Homework' 카테고리의 다른 글
| 데이터 테이블 만들고 연동하기 연습 (0) | 2023.09.10 |
|---|---|
| 활쏘기 연습-궁수의 전설 (0) | 2023.08.20 |
| Unity-Homework-몬스터 이동&공격(수정중) (2) | 2023.08.06 |
| 미션-보상 만들기 (2) | 2023.07.31 |
| 디자인 패턴& 싱글톤 패턴,Dictionary 검색 (0) | 2023.07.26 |





